Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 300.
Высота пирамиды равна 8. Найдите объем пирамиды.
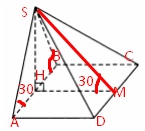
Решение
Из прямоугольного треугольника SAH
\( AH=\frac{8}{tg30}=\frac{24}{\sqrt{3}} \)
Так как SAB-р/б, то \( AB=2AH=\frac{48}{\sqrt{3}} \)
\( AD=\frac{8}{tg30}=\frac{24}{\sqrt{3}} \) – из прямоугольного треугольника \( SHM \), т.к \( HM=AD \)
\( V=\frac{1}{3}*\frac{24}{\sqrt{3}}*\frac{48}{\sqrt{3}}*8=1024 \)
Ответ: 1024
