В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками К и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ дайте в градусах.
Решение
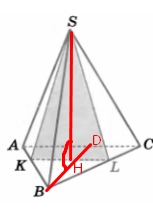
Нам нужно найти линейный угол двугранного угла SKLB
Для этого проводим два перпендикуляра из двух плоскостей \( BD \) и \( SH \), очевидно, что они пересекутся в одной точке, так как треугольник \( SKL \) – р/б, а треуг \( ABC \) – правильный.
\( ∡SHB \) – искомый угол.
Видно, из рисунка, что \( ∡SHB=90 \)
Или можно сказать, что в плоскости \( SKL \) лежит прямая, которая перпендикулярная плоскости \( ABC \) – это высота \( SH \), значит, и вся плоскость \( SKL \) будет перпендикулярная \( ABC \)
Ответ: 90
