В прямоугольном параллелепипеде ABCDA1В1C1Dl АВ=5,
AD=3, AA1=4. Найдите тангенс угла между прямыми BD1 и DC.
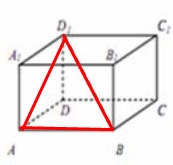
Решение
Угол между прямыми \( BD_{1} \) и \( DC \) будет равен углу между \( BD_{1} \) и \( AB \) (ну так как AB параллельна DC)
\( AD_{1} \) – перпендикулярна \( AB \) по т о 3-х перпендикулярах (\( DD1⊥AB \) \( DA⊥AB \))
треугольник \( ADD1 \) – прямоугольный
\( a=∡ABD1 \)
\( tga=\frac{AD1}{AB}=\frac{\sqrt{AD^2+DD1^2}}{AB}=\frac{\sqrt{3^2+4^2}}{5}=1 \)
Ответ: 1
