В правильной шестиугольной пирамиде сторона основания равна 4√3 , а высота равна 8. Через высоту пирамиды проведена плоскость. Найдите наименьшую площадь сечения
пирамиды такой плоскостью.
Решение
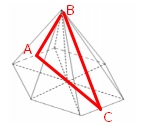
\( H=8 \)
Наименьшая площадь сечения будет тогда, когда оно будет проходить через высоты треугольников, лежащих в основании.
\( S=0.5*AC*H=0.5*12*8=48 \)
\( AC \) будет равно двум высотам правильных треугольников, и так как стороны нам известны, то найти их не составляет труда.
\( AC=2*\sqrt{(4\sqrt{3})^2-(2\sqrt{3})^2}=12 \) (высоты находим по т Пифагора. Высота в правильном треугольнике еще и медиана).
Ответ: 48
