Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной
третьему ребру, выходящему из этой же вершины.
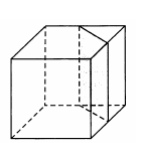
Решение
\( V=a^3=12 \)
\( V_{треугпризмы}=S_{осн}*a \)
\( S_{осн}=0.5*\frac{a}{2}*\frac{a\sqrt{2}}{4} \) – площадь равнобедренного треугольника с боковыми сторонами a/2 (по условию) и стороной основания равной половине длины диагонали квадрата. Соответственно высота треугольника по т Пифагора равна \( \sqrt{\frac{a^2}{4}-\frac{2a^2}{16}}=\frac{a\sqrt{2}}{4} \)
\( V_{треугпризмы}=\frac{a^3}{8}=\frac{12}{8}=1,5 \)
Ответ: 1,5
