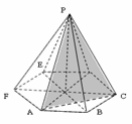
В правильной шестиугольной пирамиде PАВСDEF сторона основания равна 2, а боковое ребро равно √6. Найдите площадь сечения пирамиды плоскостью РАС.
Решение
За нас даже сделали рисунок и таким образом решили пол задачи.
\( S_{PAC}=? \)
\( S_{PAC}=0.5*AC*PH \) , где \( PH \) – высота в равнобедренном треугольнике PAC
По свойству правильного шестиугольника малая диагональ в корень и трех раз больше стороны основания \( AC=2\sqrt{3} \)
\( PH=\sqrt{6-3}=\sqrt{3} \) – по т Пифагора
\( S_{PAC}=0.5*2\sqrt{3}*\sqrt{3}=3 \)
Ответ: 3
