В правильной треугольной пирамиде сторона основания равна 42, высота равна 7√6 Найдите плоский угол при вершине пирамиды. Ответ дайте в градусах.
Решение
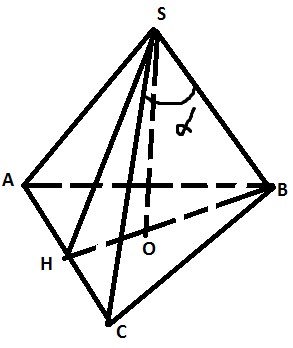
\( ∡BSC \) – искомый угол
\( BH=\frac{42\sqrt{3}}{2}=21\sqrt{3} \) – по св-ву правильного треугольника
\( BO=\frac{2}{3}BH=14\sqrt{3} \) т.к O-точка пересечения медиан.
\( SB=\sqrt{SO^2+BO^2}=21\sqrt{2} \)
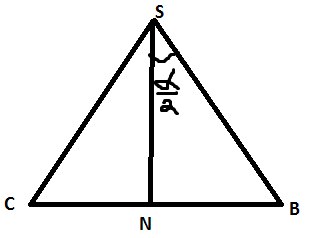
\( sin∡BSN=\frac{NB}{SB}=\frac{21}{21\sqrt{2}}\frac{\sqrt{2}}{2} \)
Значит угол ∡BSN=45°, ∡BSC=90°
Ответ: 90
