Высота правильной треугольной пирамиды втрое меньше стороны основания. Найдите угол между боковым ребром и плоскостью основания пирамиды. Ответ дайте в градусах.
Решение
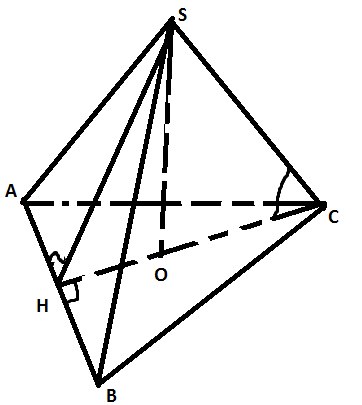
Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость.
Искомый угол \( ∡SCO \)
Пусть сторона основания равна \( a \)
\( CH=\frac{a\sqrt{3}}{2} \)
\( OC=\frac{2}{3}CH=\frac{a\sqrt{3}}{3} \) – так как O- центр треугольника, точка пересечения медиан.
\( tg∡SCO=\frac{SO}{OC}=\frac{1}{\sqrt{3}} \)
Значит сам угол 30°
Ответ: 30
