От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
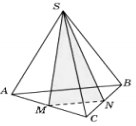
Решение
Сразу хочется поделить 12 на два и все, но это конечно же не правильно.
\( V_{0}=\frac{1}{3}S_{ABC}*h=12 \)
\( △MNC \) подобен \( △ABC \)
\( \frac{S_{ABC}}{S_{MNC}}=k^2=4 \) (думаю не надо объяснять почему k=2)
\( V_{иск}=\frac{1}{3}*S_{MNC}*h=\frac{1}{3}*\frac{1}{4}S_{ABC}*h \)
Получаем, что объем искомой пирамиды в 4 раза меньше большой пирамиды
Ответ: 3
