Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой
пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении
1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые
плоскость разбивает исходную пирамиду.
Решение
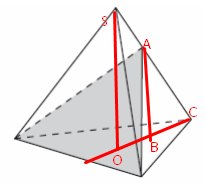
\( V=\frac{1}{3}S_{осн}*h \)
SO – высота большой пирамиды, AB- высота маленькой пирамиды
Из подобия треугольников \( △SOC \) и \( △ABC \) получаем, что \( AB=\frac{2}{3}SO \) из условия “делящей его в отношении1:2”, если SA=x, AC=2x, SC=3x)
\( V_{1}=\frac{1}{3}S_{осн}*\frac{2}{3}h=\frac{2}{3}15=10 \)
Ну и очевидно, что это больший объем
Ответ: 10
