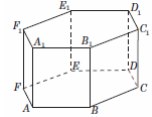
Найдите объем многогранника, вершинами которого являются вершины A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.
Решение
\( V=S_{осн}*h=6*3=18 \)
Пусть сторона основания \( a \)
\( S_{осн}=6*\frac{a^2\sqrt{3}}{4}=6 \)
\( a^2=\frac{4}{\sqrt{3}} \)
\( FC=2a \)
\( AC^2=FC^2-a^2=3a^2 \)
\( V_{FAF1A1DCD1C1}=a*\sqrt{3}*a*3=3*4=12 \)
\( V_{ABCA1B1C1}=V_{FEDF1E1D1} \)
Значит \( V_{ABCA1B1C1}=\frac{V-12}{2}=3 \)
Ответ: 3
