Площадь сечения шара плоскостью, проходящей через его
центр, равна 16. Найдите площадь сечения этого шара
плоскостью, отстоящей от его центра на расстояние, равное
половине радиуса.
Решение
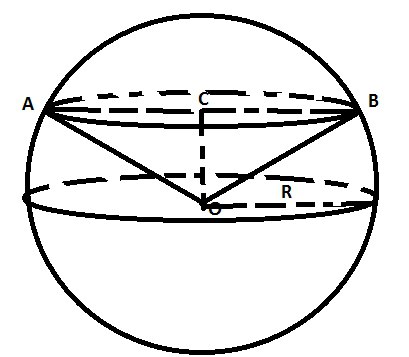
\( Sc=πR^2=16 \)
\( OC=0.5R \) – по условию
\( AC=\sqrt{R^2-\frac{1}{4}R^2}=\frac{\sqrt{3}R}{2} \) – это радиус нашего искомого сечения
\( S_{иск}=π\frac{3R^2}{4}=π\frac{3*16}{4*π}=12 \)
Ответ: 12
