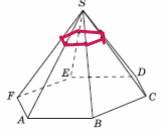
В правильной шестиугольной пирамиде SABCDEFплощадь основания равна 18, боковые ребра равны 9.Проведите сечение через точки боковых ребер,отстоящих от вершины S на расстояние 3. Найдите его площадь.
Решение
Нам нужно найти площадь правильного шестиугольника, но для этого нам нужно знать хотя бы одну его сторону
Правильный шестиугольник состоит из шести правильный треугольников
Площадь одного правильного треугольника вычисляется по формуле \( S=\frac{a^2*\sqrt{3}}{4} \)
Значит площадь правильного шестиугольника равна \( \frac{3a^2\sqrt{3}}{2} \) по условию она равна 18
Пусть \( a_{0} \) – сторона основания
\( \frac{3a_{0}^2\sqrt{3}}{2}=18 \)
Отсюда \( a_{0}^2=4\sqrt{3} \)
Через подобие треугольников не трудно понять, что сторона нашего сечения в три раза меньше, чем у основания
\( a^2=\frac{4\sqrt{3}}{9} \)
Значит \( S_{сеч}=\frac{3*4*\sqrt{3*3}}{9*2}=2 \)
Ответ: 2
