Найдите сторону основания правильной треугольной пирамиды, если её боковая
поверхность равна 72, а высота равна 2.
Решение
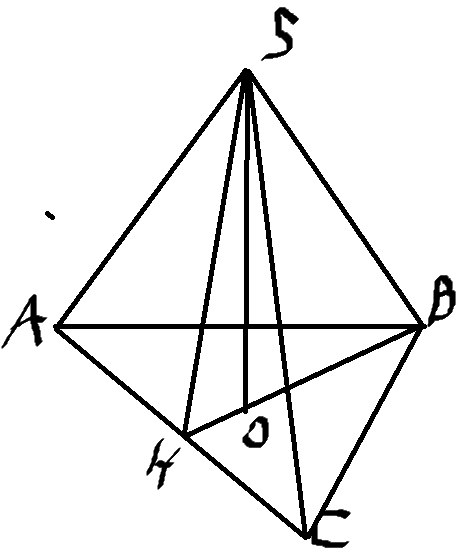
Обозначим сторону основания за \( x \)
Площадь боковой поверхности складывается из площадей трех одинаковых равнобедренных треугольников, значит площадь одного равна 72_3=24
\( S_{SAC}=24=0.5*x*SH \)
\( x=\frac{48}{SH} \)
Теперь используем нашу высоту
\( SH=\sqrt{HO^2+SO^2} \)
\( BH=\sqrt{x^2+\frac{1}{4}x}=\frac{\sqrt{3}x}{2} \)
\( SH=\sqrt{4+\frac{1}{4}x^2} \)
\( x^2=\frac{48^2}{4+\frac{1}{4}x^2} \)
Решаем биквадратное уравнение \( x^4+48x^2-27648=0 \)
Этого делать я не буду, т.к это легко.
\( x=12 \)
Ответ: 12
