Радиус основания конуса равен 3, а высота 4. Центр
шара совпадает с центром основания конуса и касается
боковой поверхности конуса. Найдите отношение объемов
шара и конуса.
Решение
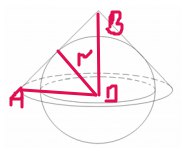
r – это радиус шара (высота проведенная к AB)
По условию AO=3, BO=4, значит AB=5 (египетский треугольник)
\( r=\frac{AO*OB}{AB}=\frac{3*4}{5}=\frac{12}{5}=2.4 \)
\( V_{ш}=\frac{4}{3}πr^3 \) а \( V_{к}=\frac{1}{3}*π*R^2*OB \)
\( \frac{V_{ш}}{V_{к}}=\frac{\frac{4}{3}*2.4^3}{\frac{1}{3}*3^2*4}=1,536 \)
Ответ: 1,536
