Ребро куба равно √6 Найдите расстояние от вершины куба до его диагонали.
Решение
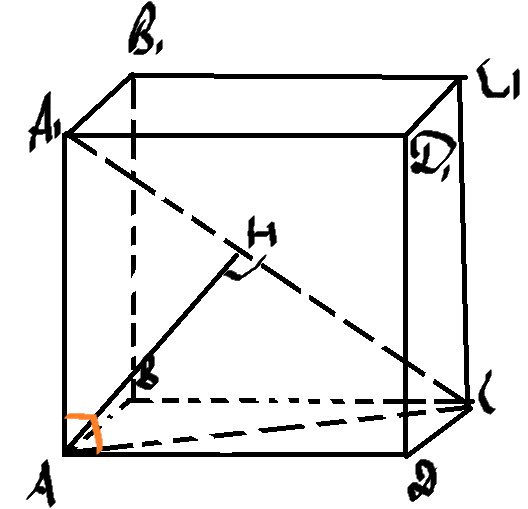
Искомое расстояние AH, найдем его из прямоугольного треугольника AA1C (AH-высота опущенная из вершины прямого угла на гипотенузу)
\( AH=\frac{AA_{1}AC}{A_{1}C} \)
\( A_{1}C=\sqrt{6+6+6}=\sqrt{18} \)
\( AC=\sqrt{AD^2+DC^2}=\sqrt{6+6}=\sqrt{12} \)
\( AH=\frac{\sqrt{6}*\sqrt{12}}{\sqrt{18}}=2 \)
Ответ: 2
