В правильной четырехугольной пирамиде боковое ребро равняется 4 и образует с плоскостью основания
угол 30. Найдите объём пирамиды.
Решение
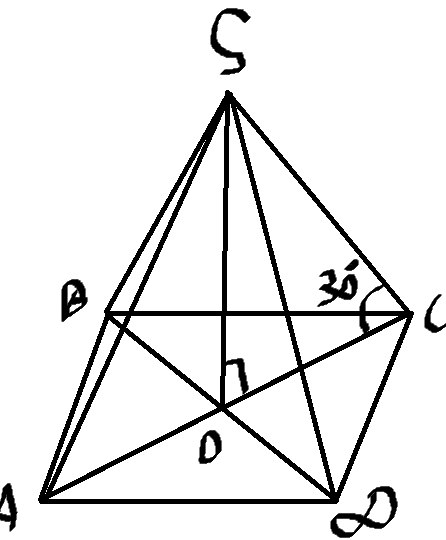
Треугольник \( OSC \) – прямоугольный. \( SC=4 \) и \( ∡OCS=30° \) – по условию
\( V_{SABCD}=\frac{1}{3}S_{осн}*SO \)
Из прямоугольного треугольника \( SO=2 \) (как катет, лежащий против угла в 30 градусов)
\( OC=\sqrt{SC^2-SO^2}=\sqrt{16-4}=2\sqrt{3} \)
\( AC=2OC=4\sqrt{3} \)
\( AC=\sqrt{2}*AD \) (по свойству диагонали квадрата) значит \( AD=4*\sqrt{\frac{3}{2}} \)
\( S_{осн}=16*1.5=24 \)
\( V_{SABCD}=\frac{1}{3}*24*2=16 \)
Ответ: 16
