Функция y=f(x) определена на промежутке (‐5;6). На рисунке изображен график ее производной. Найдите точку, в которой функция y=f(x) принимает наименьшее значение.
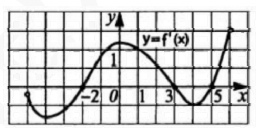
Решение
Функция будет принимать наименьшее значение там, где производная меняет знак с – на +
Таких точек целых две x=-2,5. Чисто интуитивно понятно, что в точке x=-2 значение функции будет наименьшим, т.к ф-ция долго убывала. Но это можно доказать “чисто”, используя известный вам интеграл
Из графика
\( \int_{-2}^3f'(x)dx>\int_{3}^5f'(x)dx \)
\( f(3)-f(-2)>f(5)-f(3) \)
\( f(5)>f(-2) \)
Ответ: -2
