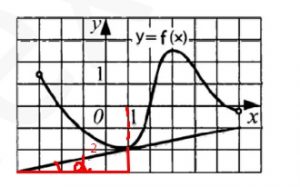
Функция y=f(x) определена на промежутке (‐3; 6). На рисунке изображен ее график и касательная к этому графику в точке с абсциссой x0=1. Вычислите значение производной функции \( y=0.5xf(x)+3x \) в точке с абсциссой x0=1.
Решение
\( y'(x)=0,5f(x)+0,5xf'(x)+3 \)
\( y'(x_{0})=0,5f(1)+0,5f'(1)+3 \)
\( f(1) \) и \( f'(1) \) можно найти из рисунка \( f(1)=-2 \)
И по геометрическому смыслу производной \( f'(1)=tg\alpha=\frac{1}{5}=0,2 \)
подставляй все в \( y'(x_{0}) \)
Ответ: 2,1
