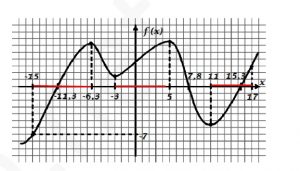
На рисунке показан график функции f(x) . Найдите на отрезке [‐15; 17] наименьшую длину промежутка, на котором совпадают знаки функции g(x)=f(x)+333 и ее производной
Решение
Из рисунка \( f(x)>=-7 \), \( g(x)=f(x)+333>=326>0 \)
\( f'(x)=g'(x) \)
Знак производной будет положителен, когда ф-ция возрастает.
Наименьшая длина отрезка (из 3-х) будет 6
Ответ: 6
