Используя геометрический смысл определенного интеграла, вычислите.
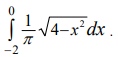
Решение
\( \int_{-2}^{0} \frac{\sqrt{4-x^2}}{\pi} dx=\frac{1}{\pi} \int_{-2}^{0} \sqrt{4-x^2} dx= \)
По сути \( \sqrt{4-x^2} \) – это уравнение окружности, с радиусом 2 ( \( x^2+y^2=r^2 \) )
Причем нам дана верхняя часть этой окружности и нужно найти площадь 1/4 круга
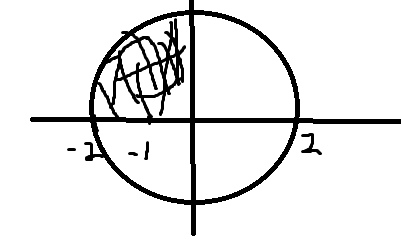
\( \frac{1}{\pi}*\frac{1}{4}*\pi2^2=1 \)
Ответ: 1
