Функция y=f(x) определена на промежутке (—3;7). На рисунке изображён график её производной y=f'(x) Найдите число касательных к графику функции y=f(x), которые наклонены под углом 150° к положительному направлению оси абсцисс.
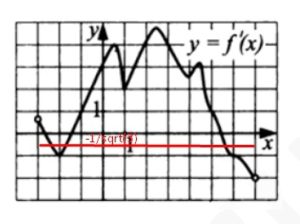
\( f'(x0)=tg150=tg(180-30)=-tg30=-\frac{1}{\sqrt{3}} \)
Строим прямую \( y=-\frac{1}{\sqrt{3}} \) и считаем кол-во точек пересечения с графиком
Ответ: 3
