На рисунке изображен график \( y=f'(x) \)-производной функции f(x) , определенной на интервале (-6;8). Сколько можно провести касательных к графику функции f(x) которые образуют угол 45 с прямой x=0?
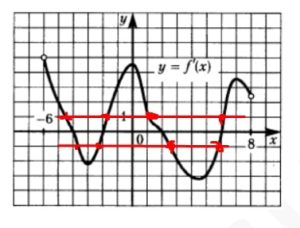
Решение
По геометрическому смыслу производной
\( f'(x_{0})=tg\alpha=tg45=1 \)
Но нас будут устраивать две прямые
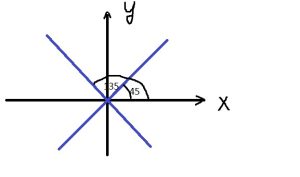
Т.к они обе образуют с прямой x=0 угол 45
\( f'(x_{0})=tg\alpha=tg135=-1 \)
Значит нам нужно найти количество точек пересечения графика с прямой \( y=-1 \) и \( y=1 \)
Ответ: 8
