Дан треугольник ABC площади 1. На продолжении его стороны AB за точку B выбрана точка K так, что AB = BK. На продолжении BC за точку C выбрана точка L так, что BC =CL, а на продолжении CA за точку A—точка M так, что CA= AM. Найдите площадь треугольника KLM.
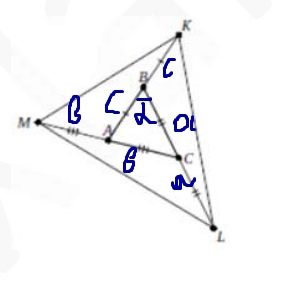
Решение
\( S_{ABC}=0.5*a*c*sin\alpha=1 \)
\( S_{KBL}=0.5*2a*c*sin(180-\alpha)=2*a*c*sin\alpha=2 \)
Аналогично с остальными треугольниками, в качестве альфа естественно выбираем другие углы, который будут удобны.
\( S_{ABC}=0.5*a*b*sinBCA=1 \)
\( S_{ABC}=0.5*a*2b*sin(180-BCA)=2 \)
и тд
Ответ: 7
