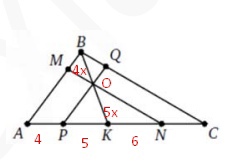
На сторонах AB и BC треугольника ABC выбраны соответственно точки M и Q, а на стороне AC —точки P, K, N (именно в таком порядке, считая от A) таким образом, что MN || BC, PQ || AB и KB проходит через точку пересечения MN и PQ. Известно, что AP =4, PK =5 и KN =6. Найдите NC
Решение
Параллельные прямые делят стороны угла на пропорциональные отрезки, значит
\( \frac{AP}{PK}=\frac{BO}{OK} \) и \( \frac{KN}{NC}=\frac{OK}{BO} \)
Запишем
\( \frac{KN}{NC}=\frac{5}{4}=\frac{6}{NC} \)
\( NC=4,8 \)
Ответ: 4,8
