На основании равнобедренного треугольника построен правильный треугольник, площадь которого в 3 раза больше площади данного. Найдите наибольший угол исходного треугольника. Ответ дайте в градусах.
Решение
Тут можно рассмотреть несколько случаев, когда высоты треугольников лежат по одну сторону от AC и нет. Но ответ конечно же не изменится.
Рассмотрим такой рисунок, когда B и B1 находится на противоположных сторонах (остальные случаи рассматриваются аналогично)
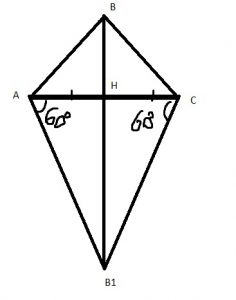
\( \frac{S_{AB1C}}{S_{ABC}}=\frac{0.5AC*B1H}{0.5AC*BH}=\frac{B1H}{BH}=3 \)
Так как AB1C- равносторонний, то все его углы по 60, и высота – это и медиана и биссектриса
\( tg60=\frac{B1H}{AH} \)
\( B1H=tg60*AH=\frac{\sqrt{3}}{2}AC \) (AH=0.5AC)
Значит \( BH=\frac{AC}{2\sqrt{3}} \)
\( tg∠BAH=\frac{BH}{0.5AC}=\frac{1}{\sqrt{3}} \)
Значит \( ∠BAH=30 \)
и значит наибольший угол будет \( ∠ABC=180-(30+30)=120 \)
Ответ: 120
