В трапеции KLMT LM II KT, KL = MT, диагональ МК = 8 и ∠MKT=75°. Найдите площадь трапеции.
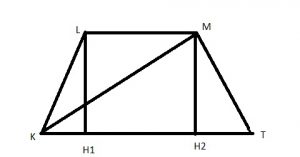
Решение
\( S=\frac{LM+KT}{2}*MH2 \)
\( KH1=TH2=\frac{KT-LM}{2} \) – по св-ву р\б трапеции
\( KH2=KT-TH2=KT-\frac{KT-LM}{2}=\frac{LM+KT}{2} \)
Из KMH2
\( MH2=sin75*KM=8sin75° \)
\( KH2=8cos75 \)
\( S=KH2*MH2=64sin75°*cos75°=32sin150°=\)
\( =32sin(180°-30°)=32sin30°=16 \)
Ответ: 16
