Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС в точках Т и М соответственно. Найдите ТМ, если АВ = 25, ВС = 14.
Решение
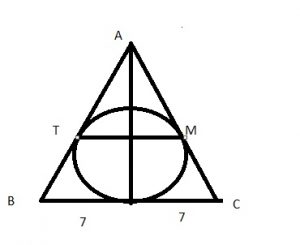
Отрезки касательных проведенных к окружности из одной точки равны. Значит \( BT=BH=7 \) и \( CM=CH=7 \)
\( AT=25-7=18 \) и \( AM=25-7=18 \)
треугольник \( ATM \) подобен \( ABC \) по углу и пропорциональным сторонам из этого \( \frac{TM}{BC}=\frac{18}{25} \), (BC=14), отсюда
\( TM=10,08 \)
Ответ: 10,08
