В правильном треугольнике АВС проведена средняя линия DE параллельно АС. Прямая, проходящая через точку А и середину F отрезка DE, пересекает ВС в точке К. Найдите длину отрезка АК, если AC=9√7
Решение
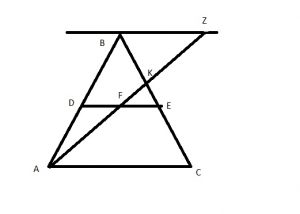
Сделаем доп. построение. Построим прямую || AC из точки B, продолжим прямую AK до пересечения с этой прямой. Пусть они пересекаются в точке Z.
AK-легче всего найти из треугольника ABK по т косинусов (угол B=60, т.к равносторонний треугольник). Но нам нужно знать BK
\( ▲BKZ \) подобен \( ▲EKF \) – по 2-м углам
\( BZ=2DF \) (DF-средняя линия треугольника ABZ)
значит \( \frac{BK}{KE}=\frac{BZ}{FE}=2 \)
\( BK=2KE \)
\( BE=BK+KE=3KE \), откуда \( KE=\frac{1}{3}BE \) и \( BK=\frac{2}{3}BE \) (BE=0,5BC=0,5AC)
Мы все знаем, применяем т косинусов
\( AK^2=AB^2+BK^2-2AB*BK*cos(60) \)
Подставляя все известные нам данные получаем ответ
Ответ: 21
