Точка пересечения биссектрис делит одну из биссектрис треугольника в отношении 2020:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 2021.
Решение
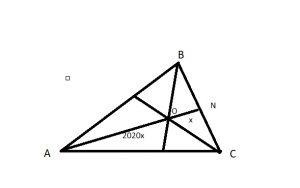
\( \frac{AO}{ON}=\frac{2020}{1} \)
Рассмотрим треугольник ABN, в нем исходя из св-в биссектрисы \( \frac{AB}{BN}=\frac{AO}{ON}=\frac{2020}{1} \)
Можно аналогично рассмотреть треугольник ANC, и из него \( \frac{AC}{CN}=\frac{AO}{ON}=\frac{2020}{1} \)
Т.е \( AB=2020x \), \( BN=x \), \( AC=2020y \), \( CN=y \)
\( BC=BN+NC=2021 \) по условию
\( x+y=2021 \)
\( P=2021(x+y)=4084441 \)
Ответ: 4084441
