Сторона правильного шестиугольникаABCDEF равна 2020√3 . Найдите радиус окружности, вписанной в треугольник MPK, если точки М, Р и К – середины сторон АВ, CD, EF соответственно.
Решение
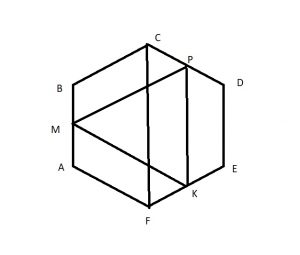
Для удобства обозначим \( 2020\sqrt{3}=a \)
Пусть \( O \) – центр нашего шестиугольника
\( OC=OF=R=a \) – по св-ву правильного шестиугольника
Рассмотрим трапецию \( CDEF \). В ней \( PK \) – средняя линия по построению
\( PK=\frac{a+2a}{2}=1,5a \) – средняя линия трапеция равна полу сумме оснований
Аналогично и с другими сторонами (рассматривая трапеции ABCD и BCDE). Т.е треугольник \( MPK \) – равносторонний
\( R=\frac{S}{p} \)
\( p=\frac{a+a+a}{2}=1,5a \)
\( S=\frac{a^2\sqrt{3}}{4} \)
Пользуясь данными формулами можно получить ответ
Ответ: 1515
