В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5. Определите площадь треугольника.
Решение
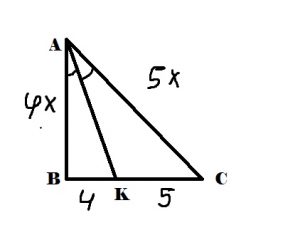
Вспоминаем свойство биссектрисы: она делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника
\( \frac{4}{5}=\frac{AB}{AC}=\frac{4x}{5x} \)
По т Пифагора \( AC^2=BC^2+AB^2 \)
\( 25x^2=16x^2+81 \)
откуда \( x=3 \)
\( S=0.5*BC*AB=0.5*9*12=54 \)
Ответ: 54
