В равнобедренном треугольнике MNK (NK = MK) проведены высоты MP и NF. Известно, что PF = 3, а косинус угла К равен 0,3. Найдите длину стороны MN.
Решение
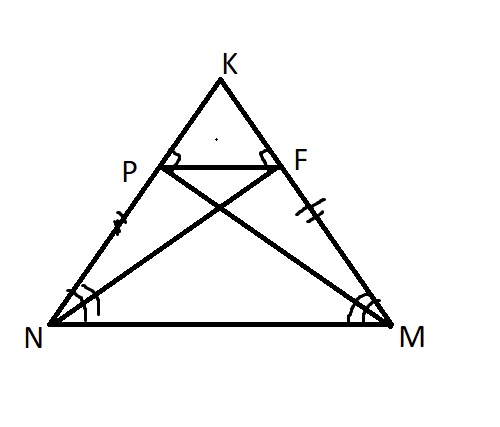
Заметим, что треугольники \( △NPM=△MFN \) (по стороне и 2-м углам). т.к \( NM \) – общая сторона, и два угла соотвественно равны из условия.
Значит мы можем утверждать, что \( NP=FM \), а значит и \( KP=KF \)
Т.е получаем пропорциональные отрезки. Можем сказать, что \( △KPF \) подобен треугольнику \( △KNM \) в силу пропорциональности сторон и общего угла.
Рассмотрим прямоугольный треугольник \( △KNF \) и вспомним про косинус, не зря же он нам дан.
Соотвественно \( cos∠K=\frac{KF}{KN}=0,3 \)
А из этого не трудно найти NM:) Думаю, вы сами знаете как это сделать (воспользоваться соотношением\( \frac{PF}{NM}=\frac{KF}{KM}=0,3 \))
Ответ: 10
