На сторонах АВ и ВС треугольника АВС взяты соответственно точки M и N так, что AM : MB = 2 : 3 и BN : NC = 4 : 9. Найдите площадь четырехугольника AMNC, если площадь треугольника АВС равна 130.
Решение
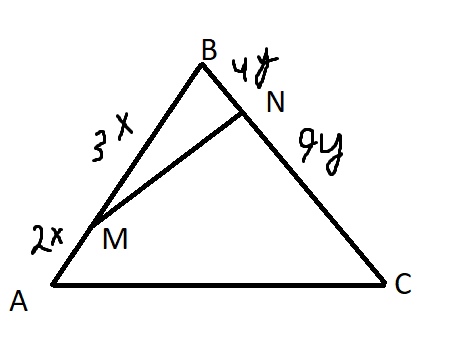
\( S_{AMNC}=S_{ABC}-S_{BMN} \)
Осталось найти площадь треугольника BMN)
Но сделать это легко, т.к треугольники ABC и BMN подобны по 2-му признаку подобия, значит для их площадей можно записать равенство
\( \frac{S_{BMN}}{S_{ABC}}=\frac{0,5*sin(∠B)*BM*BN}{0,5*sin(∠B)*BA*BC}=\frac{BM*BN}{BA*BC}=\frac{3x*4y}{5x*13y}=\frac{12}{65} \)
Откуда \( S_{BMN}=\frac{12S_{ABC}}{65}=\frac{65*130}{12}=24 \)
\( S_{AMNC}=130-24=106 \)
Ответ: 106
