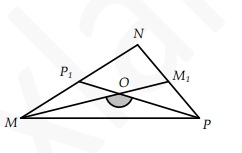
В треугольнике MNP известно, что МM1 и РР1 ‐ медианы MM1=9√3,PP1=6, ∠MOP=150.Найдите радиус окружности, описанной около треугольника МОР.
Решение
\( R=\frac{abc}{4S} \)
Что нужно знать, так это то, что медианы в точке пересечения делятся в отношении 2:1 считая от вершины.
Значит мы с легкостью можем найти OP и OM (\( OP=\frac{2}{3}PP1=4 \) и \( OM=\frac{2}{3}MM1=6\sqrt{3} \)). Осталось найти MP.
Но нам не просто так дан угол! Применяем т Косинусов и находим MP. \( MP^2=OM^2+OP^2-2*OM*OP*cos(MOP) \) , \( MP=14 \)
Теперь мы знаем все стороны! Значит знаем и площадь. \( S=0,5*4*6\sqrt{3}*sin(150)=6\sqrt{3} \)
\( R=\frac{4*6\sqrt{3}*14}{4*6\sqrt{3}}=14 \)
Ответ: 14
