Длины диагоналей трапеции равны 9 и 12, а длина ее средней линии равна 7,5. Найдите площадь трапеции.
Решение
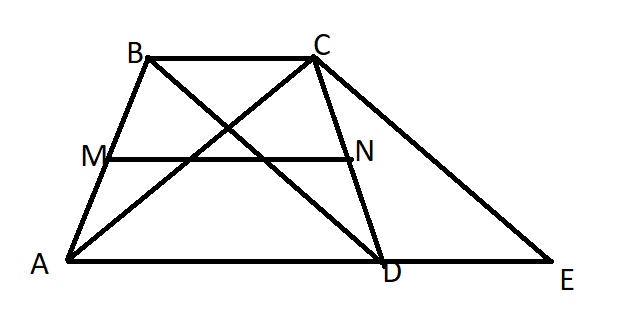
Проведем из точки С прямую параллельную BD.
Заметим, что BDCE – параллелограмм по построению.
\( MN=\frac{BC+AD}{2}=7,5 \) Значит \( BC+AD=15 \)
\( S_{ABCD}=\frac{BC+AD}{2}*h \)
\( S_{ACE}=\frac{AE*h}{2} \), но \( AE=AD+DE=AD+BC \), т.е \( S_{ACE}=\frac{BC+AD}{2}*h=S_{ABCD} \)
Заметим, что треугольник ACE со сторонами 9,12,15 (образуют пифагорову тройку) -прямоугольный.
Значит \( S_{ACE}=0,5*9*12=54 \)
Ответ: 54
