Найдите площадь правильного двенадцатиугольника, если его сторона равна \( 6\sqrt{2-\sqrt{3}} \)
Решение
Если опишем окружность и проведем радиусы, то площадь правильного двенадцатиугольника будет равна сумме площадей 12 равнобедренных треугольников.
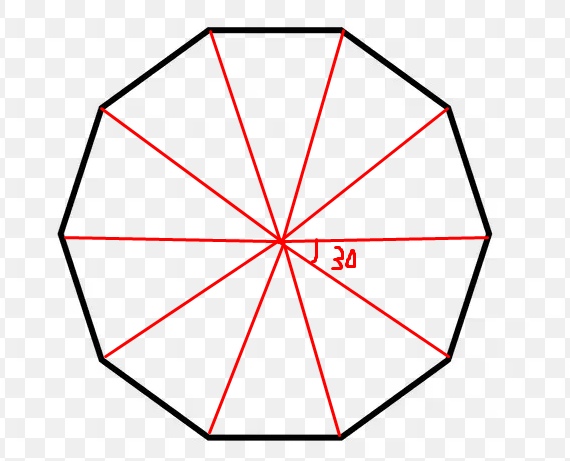
Нам нужно найти радиусы r.
Нам известен угол, по т косинусов можно выразить r
\( 36*(2-\sqrt{3})=r^2+r^2-2r^2*cos30 \)
Получаем квадратное уравнение) \( r=6 \)
\( S_{1}=0,5*r*r*sin30=\frac{36}{4}=9 \)
И \( S_{12}=12*9=108 \)
Ответ: 108
