В равнобедренном треугольнике АВС с основанием АС высоты ВМ и АН пересекаются в точке К, причем АК=5, КН=3. Найдите площадь треугольника АВК.
Решение
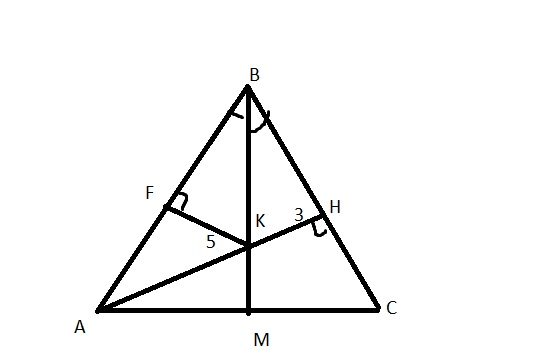
BM – биссектриса и высота, т.к треугольник равнобедренный по условию
По св-ву биссектриссы, \( KF=KH=3 \), значит \( BF=BH \)
По т Пифагора \( AF=\sqrt{AK^2-KF^2}=4 \)
По св-ву биссектрисы \( \frac{AK}{KH}=\frac{AB}{BH}=\frac{5}{3} \)
\( AB=BC \)
\( AB=BH+HC \)
\( AB=BH+4 \) (AF=HC=4)
\( \frac{BH+4}{BH}=\frac{5}{3} \)
\( BH=6 \)
и значит \( AB=4+6=10 \)
\( S_{AKB}=0,5*KF*AB=0,5*3*10=15 \)
Ответ: 15
