Дан ромб ABCD с острым углом B. Площадь ромба равна 320, а синус угла В равен 0,8. Высота СН пересекает диагональ BD в точке К. Найдите длину отрезка СК.
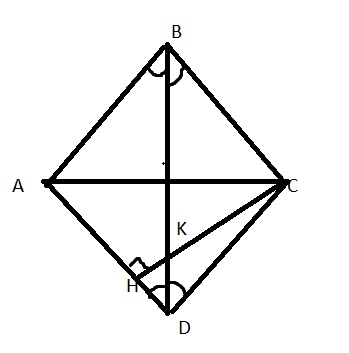
Решение
Пусть сторона ромба \( a \)
\( S=a^2*sinB=320 \), откуда \( a=20 \)
\( sinD=\frac{CH}{a} \), помним, что противоположные углы у ромба равны, значит \( sinB=sinD \)
\( CH=sinD*a=16 \)
\( DH=a*cosD=a*\sqrt{1-sin^2D}=12 \)
Рассмотрим прямоугольный треугольник CHD, в нем DK-биссектрисса. Вспомним свойство биссектриссы
\( \frac{KH}{DH}=\frac{CK}{DC} \)
Из этой пропорции можно легко найти \( CK=DC*\frac{KH}{DH} \) (обозначив \( CK=x \), тогда HK=16-x)
\( CK=10 \)
Ответ: 10
