Найдите периметр параллелограмма ABCD, если AD=10, BD=8, а отрезок, соединяющий вершину В с серединой стороны AD, равен √15
Решение
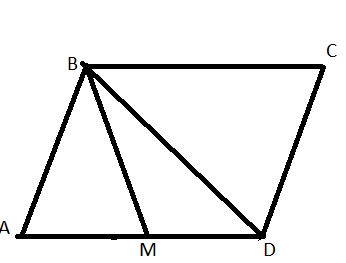
\( BM^2=\frac{1}{4}(2*BD^2+2*AB^2-AD^2)=\frac{1}{4}(2*8^2+2AB^2-10^2)=15 \) – ф-ла медианы
\( AB=4 \)
\( P=2*4+2*10=28 \)
Ответ: 28
