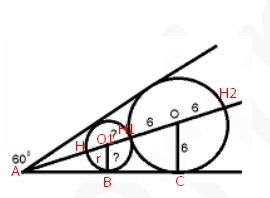
Центр О окружности радиуса 6 принадлежит биссектрисе угла 60. Найдите радиус окружности, вписанной в данный угол и касающейся данной
окружности, как показано на рисунке.
Решение
\( AO=\frac{6}{sin30}=12 \) – из прямоугольного треугольника
\( AC=12*cos30=6\sqrt{3} \)
из подобия двух треугольников можно получить соотношения
\( \frac{r}{6}=\frac{AH+r}{AH+2r+6} \)
По т. касательной и секущей получаем:
\( AC^2=AH1*AH2=(AH+2r)(AH+2r+12)=36*3=108 \)
Получили систему из 2-х неизвестных решаем ее)
\( (r,AH)=(2,2) \)
\( (r,AH)=(18,-54) \)
-эта пара не подходит, т.к длина отрезка не может быть отрицательной
Ответ: 2
