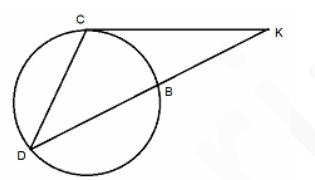
На окружности в последовательном порядке заданы точки B, C, D. Касательная к окружности, проведенная через точку С и продолжение хорды DB пересекаются в точке К. Найдите хорду DC, если ∠DKC=60, KB_BD=4:5, KC=12. В ответе укажите значение DC*√7
Решение
\( KB_BD=4:5 \) Пусть \( KB=4x,BD=5x \)
по теорема о касательной и секущей получаем
\( CK^2=KB*KD \)
\( 144=4x*9x \)
\( x=2 \)
по т косинусов из треугольника CKD
\( DC^2=CK^2+DK^2-2CK*DK*cos60 \)
\( DC*\sqrt{7]=42 \)
Ответ: 42
