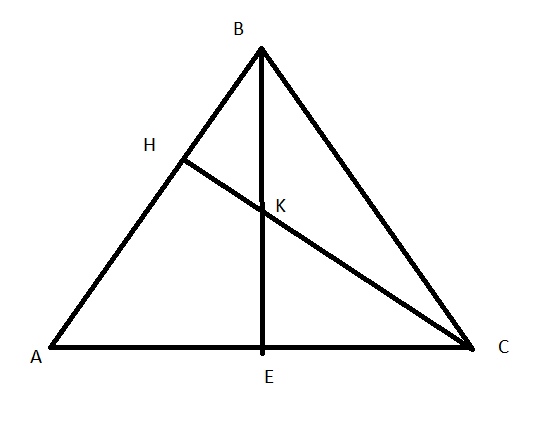
В равнобедренном треугольнике АВС с основанием АС высоты ВЕ и СН пересекаются в точке К, причем ВН=6, КН=3. Найдите площадь треугольника СВК.
Решение
\( S_{CBK}=0,5*BH*CK \), нужно найти CK
\( tg(∠\frac{B}{2})=\frac{HK}{BH}=0,5 \)
\( tg(∠B)=tg(∠\frac{B}{2}+∠\frac{B}{2})=\frac{tg(∠\frac{B}{2})+tg(∠\frac{B}{2})}{1-tg(∠\frac{B}{2})*tg(∠\frac{B}{2})}=\frac{4}{3} \)
\( tg(∠B)=\frac{CK+KH}{BH}=\frac{4}{3} \)
\( CK=5 \)
\( S_{CBK}=0,5*6*5=15 \)
Ответ: 15
