В треугольнике ABC угол C равен 90°, CH – высота, угол В равен 60°, AB = 10. Найдите АH.
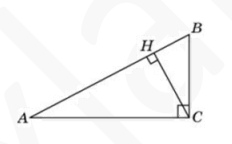
Решение
\( AC=10*sin60=5\sqrt{3} \)
\( BC=10*cos60=5 \)
\( S=0,5*AC*BC=0,5*AC*CH \)
\( CH=\frac{25*\sqrt{3}}{10}=2,5\sqrt{3} \)
и по т Пифагора \( AH=\sqrt{AC^2-CH^2}=7,5 \)
Ответ: 7,5
