Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен \( \frac{\sqrt{2}}{10} \)
Решение
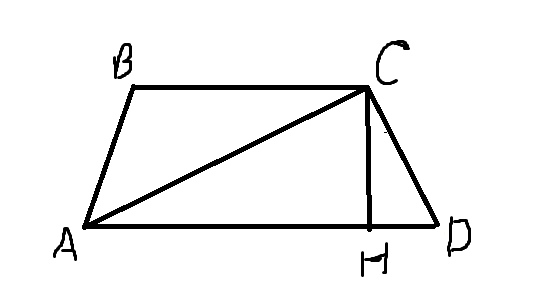
\( AC=10 \)
\( AH=\frac{\sqrt{2}}{10}*10=\sqrt{2} \)
\( AH=\frac{BC+AD}{2} \)
\( CH=\sqrt{100-2}=\sqrt{98}=7\sqrt{2} \) из прямоугольного треугольника
\( S=\frac{AD+BC}{2}*CH=7\sqrt{2}*\sqrt{2}=14 \)
Ответ: 14
