В треугольнике площадью 70 биссектриса AD делит сторону ВС на отрезки BD и DC, причем BD_DC=3:2. На стороне АС выбрана точка К такая, что биссектриса AD пересекает ВК
в точке Е и BE_EK=5:2. Найдите площадь четырехугольника EDCK.
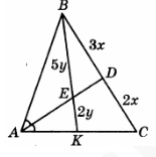
Решение
\( S_{EDCK}=S_{BKC}-S_{BED} \)
Вспоминаем свойство биссектрисы
\( \frac{AB}{AC}=\frac{3}{2} \)
\( \frac{5}{2}=\frac{AB}{AK} \)
делим одно на другое
\( AK=\frac{3}{5}AC \)
Значит \( S_{ABK}=\frac{3}{5}S_{ABC}=42 \) (т.к у них одинаковые высоты, отличаются лишь основания)
\( S_{BKC}=70-42=28 \)
Осталось найти \( S_{BED} \)
\( S_{BED}=S_{ABD}-S_{ABE} \)
\( \frac{S_{ABD}}{S_{ADC}}=\frac{3}{2} \) , т.к у них также равны высоты.
\( S_{ABD}=\frac{3}{5}S_{ABC}=42 \)
\( \frac{S_{ABE}}{S_{AEK}}=\frac{AB}{AK}=\frac{5}{2} \)
\( S_{AEK}=\frac{2}{5}S_{ABE} \)
и значит \( S_{ABE}=\frac{5}{7}S_{ABK}=\frac{5}{7}*42=30 \)
\( S_{BED}=42-30=12 \)
\( S_{EDCK}=28-12=16 \)
Ответ: 16
