Найдите радиус окружности, вписанной в правильный шестиугольник, периметр которого равен 12√3
Решение
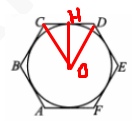
\( OH \) искомый радиус вписанной окружности
\( OH=\sqrt{a^2-\frac{a^2}{4}}=\frac{a\sqrt{3}}{2} \) – по т Пифагора из прямоугольного треугольника
\( P=6*a=12\sqrt{3} \)
\( a=2\sqrt{3} \)
\( OH=3 \)
Ответ: 3
