Медианы прямоугольного треугольника, проведённые к катетам, равны 2√13 и √73. Найдите длину медианы, проведённой к гипотенузе.
Решение
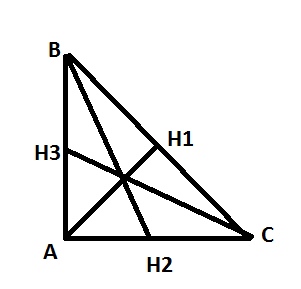
По условию \( BH2=\sqrt{73} \) и \( CH3=2\sqrt{13} \) или наоборот не имеет разницы.
Применим теорему Пифагора
\( BH2^2=AB^2+\frac{AC^2}{4}=73 \)
\( CH3^2=AC^2+\frac{AB^2}{4}=4*13 \)
Решаем систему из 2-х неизвестных и получаем, что
\( BH2^2=64 \)
\( CH3^2=36 \)
Значит \( BC^2=100 \) или \( BC=10 \)
По свойству прямоугольного треугольника, медиана проведенная к гипотенуза равна половине гипотенузы
Ответ: 5
