Основания равнобедренной трапеции равны 6 и 8, а радиус описанной вокруг неё окружности равен 5. Центр окружности лежит вне трапеции. Найдите высоту трапеции.
Решение
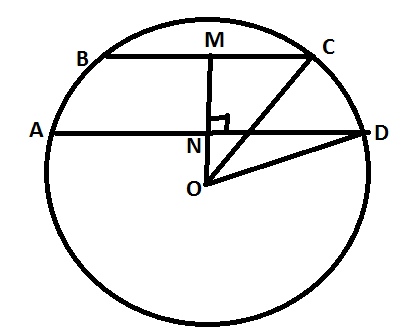
\( MN \) – высота трапеции
\( M,N \) – это середины соответствующих сторон.
\( OM=\sqrt{OC^2+MC^2}=\sqrt{5^2-3^2}=4 \)
\( ON=\sqrt{5^2-4^2}=3 \)
\( MN=OM-ON=4-3=1 \)
Ответ: 1
