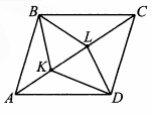
В параллелограмме ABCD на диагонали АС взяты точки К и L так, что AK=1/3AC, CL=0,4AC. Найдите площадь четырехугольника BLDK, если площадь параллелограмма ABCD равна 45.
Решение
\( S_{ABCD}=0,5*BD*AC*sinw \), где \( w \) – угол между диагоналями, т.е между AC и BD
\( S_{BLKD}=0,5*BD*KL*sinw \)
\( KL=AC-(AK+CL)=\frac{4}{15}AC \)
Тогда площадь \( BLKD \) в \( \frac{4}{15} \) раз меньше, чем площадь \( ABCD \)
Ответ: 12
